5. Statistical Tests III – Statistical models continued
Previously in this set of articles focusing on using R to perform statistical tests I introduced the topic of statistical models and how to apply a simple linear model to two continuous variables, a linear regression. As I mentioned previously, statistical modelling is a wide subject that could easily fill the next couple of years’ worth of articles. Therefore, in this last article on statistical methods I will be covering two other commonly used statistical modelling techniques, multiple linear regression and Analysis of Variance (ANOVA).
Multiple linear regression
In the regression example, we were interested in examining the relationship between our dependent variable against a single independent variable. However, there may be occasions when you have more than one independent variable that you want to include in your model; here you will need multiple linear regression.
To illustrate how to implement a multiple linear regression we will turn to the extrinsic dataset that we’ve used regularly throughout this series. The first step, as always, is to load the file into the R environment creating the new variable extrinsic:
extrinsic <- read.table(file="extrinsic.txt", header=TRUE)In this case we want to know if there is a relationship between variables representing the amount of rock record sampled (Rock.area_sum), the evenness of environmental sampling (evenness), and environmental fluctuations (Temperature and CO2) with a measure of sample-corrected diversity. The latter will be the dependent variable in this study and has been calculated using shareholder quorum subsampling method (SQS) of Alroy (2010).
If you open up the entire extrinsic dataset you will see that there are missing entries in some places. A quick and simple fix for this issue is to remove the most recent time-bin, which in this case is the last row in the dataset that has 51 rows, so we can simply ask for rows 1 through to 50 and place this in the new variable extrinsicLM:
extrinsicLM <- extrinsic[c(1:50),]In this case, the selecting of specific rows works with this dataset; however, it is more likely that gaps in a dataset will not be so evenly spaced. Happily there is a quick way to retain all the rows with complete entries for the columns you are interested in. The function complete.cases, used as follows, will return an array detailing which rows are complete (marked as TRUE) and those which are not (marked as FALSE):
complete.cases(extrinsic)Remember that the format for selecting a section of a dataframe is with the row followed by the column such as dataframe[row , column]. So, in order to get the rows that are complete, we can place this logical statement into the row part of the dataframe:
extrinsicLM <- extrinsic[complete.cases(extrinsic), ]To clarify this operation: the R command complete.cases(complete) converts your data to an array containing values that are either TRUE or FALSE, and returns only the rows that are marked as TRUE. As an aside, if you have a much larger dataset and need to know where your missing data are, and therefore want R to return the rows of a dataset where there are missing data, you can add an exclamation mark ‘!’ in front of the command – !complete.cases – or add a logical conditional statement such as:
extrinsic[complete.cases(extrinsic) == FALSE,]If you run this, you will see that R will return the rows with any missing data; in this case there are three such rows.
Anyway, getting back on track, now that we are selecting the rows we want we can also use the change to restrict the data to just the columns we want to examine. This is not necessary, but can be useful when working with and plotting large datasets. So now we will create a new variable, extrinsicLM, containing just the rows and columns that we need for this analysis, using the following:
extrinsicLM <- extrinsic[complete.cases(extrinsic), c("SQS", "evenness", "Temperature", "CO2", "Rock.area_sum")]As always, plot your data first to get an idea of any issues with the dataset such as outliers, or if there are any trends within the dataset. A handy function for creating multiple scatter plots when you have a lot of variables in your dataset is pairs; this will create bivariate plots for all pairs of variables that you are interested in:
pairs(extrinsicLM)As we have already restricted the file to the variables we want, this makes for an easy-to-read five by five grid of scatter plots (Figure 5.1). From this you can see that, when comparing our diversity value (first column, SQS) with our other variables, the evenness variable at first glance appears to show a positive relationship while other combinations show little relationship, as in the case with SQS and Temperature or a non-linear relationship as in Temperature and CO2.
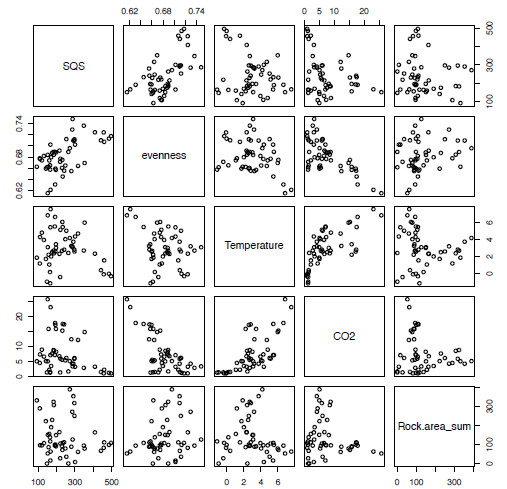
Figure 5.1. A series of bivariate plots representing all pair-wise combinations of the variables from the extrinsic variables of interest in the multiple linear regression analysis.
Right, moving on to the analysis, the ultimate aim for a multiple regression is to determine which combination of independent variables can be best used to predict our dependent variable, here a measure of sample-corrected diversity. So, the first step is to include all of the variables in the model formulae. Here we can use the same function we used for the linear regression, lm, and to make it easier to follow we can just use the column names we wish to include, providing we tell R where the data are using the argument data:
model.lm <- lm(SQS ~ evenness + Temperature + CO2 + Rock.area_sum, data = extrinsicLM)The function summary can be used to get a description of this model:
summary(model.lm)
Call:
lm(formula = SQS ~ evenness + Temperature + CO2 + Rock.area_sum, data = extrinsicLM, na.action = na.exclude)
Residuals:
Min 1Q Median 3Q Max
-121.334 -47.620 -8.036 44.181 182.580
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -1419.7219 369.0615 -3.847 0.000391 ***
evenness 2424.6739 535.0964 4.531 4.62e-05 ***
Temperature -4.9951 7.5796 -0.659 0.513396
CO2 5.0093 3.1368 1.597 0.117605
Rock.area_sum -0.1992 0.1074 -1.854 0.070561 .
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 69.95 on 43 degrees of freedom
Multiple R-squared: 0.3717, Adjusted R-squared: 0.3132
F-statistic: 6.359 on 4 and 43 DF, p-value: 0.0004117You can see from the last line here that the p-value shows that there is an overall significant relationship between our dependent variable and independent variables. However, not all of the variables fit as well if we examine the last column under “Coefficients” which shows that Temperature and CO2 variables are not significant. As we want there to be only significant variables in the model we can systematically remove them one at a time, starting with the least significant variable, Temperature in this case (p = 0.51). Here we will use the same syntax below but removing the relevant variable:
model.lm2 <- lm(SQS ~ evenness + CO2 + Rock.area_sum, data = extrinsicLM)If we now call for the same summary(model.lm2) we will see that the model has become slightly more significant overall, but the CO2 variable still remains as non-significant so we can again remove this to leave just the evenness and Rock.area_sum variables:
model.lm3 <- lm(SQS ~ evenness + Rock.area_sum, data = extrinsicLM)Finally, looking at the summary for this model (summary(model.lm3)) you will see that we now only have a model with significant variables, although Rock.area_sum is only significant with a p < 0.1 rather than a more acceptable p < 0.05. However, if we look at the adjusted R-squared values for these three models it is model.lm2 that has the highest value, meaning that this model is explaining more of the variation seen in our dependent variable, so perhaps it is the best model overall. We’ll come back to this in a moment. In summary, here we have created three models (model.lm, model.lm2, model.lm3) each of which represents a single multiple linear regression. However, through the sequential removal of the least significant terms we have performed a statistical technique called stepwise multiple linear regression. As a point of interest, this method is considered by some to have some significant pitfalls (Whittingham et al. 2006).
Akaike information criterion, an alternative method for model selection
An alternative to the approach described above is to use the Akaike information criterion (AIC), which we will come to more in later articles when I discuss comparing models across phylogenies. The AIC is a measure of the ‘goodness of fit’ of a model and can be used to directly compare a series of models. Importantly, this method shouldn’t be used to compare models across different datasets. We can get the AIC value for each of our models by using the function AIC as follows:
AIC(model.lm)
[1] 550.7193
AIC(model.lm2)
[1] 549.2017
AIC(model.lm3)
[1] 549.9476The AIC value is calculated using the following equation:
\[\text{AIC} = 2K – 2ln(L)\]
Here L represents the likelihood of the model and \(K\) is the number of free parameters (explanatory variables) in the model. In essence the first parameter here (\(2K\)) penalises a model for being more complex, i.e. having more free variables. The best model is the one with the lowest AIC value, so in the case of the three models we’ve already fitted you can see that model.lm has the highest value and therefore the least fit to the data when compared with the other two models. Of model.lm2 and model.lm3 the former has a slightly better fit; if you remember from our stepwise removal of values, this is the model that also has a higher adjusted R-squared value.
Rather than removing each variable in turn, there is a function that will automate this and provide the model that fits best; it is called step, and for this you only require the model with all of the variables included.
model.lm.step <- step(model.lm)This will return a lot of information as it tries out various combinations of variables, but it is the output at the bottom that we are interested in. Here it provides the formula for the best model, which you may notice is the same as we used for model.lm2.
Currently we have examined models containing four, three and two independent variables by successively removing the least significant variables in turn. However, if we look at summary(model.lm3) that contains two independent variables we can see that the evenness variable is far more significant than the Rock.area_sum variable. In this case it may be worth checking to see whether a model containing evenness as a sole independent variable may be a better fit that the current best fit model, i.e. model.lm2. So now we can follow the procedure from before and create the variable model.lm4 containing the new model:
model.lm4 <- lm(SQS ~ evenness, data = extrinsicLM)Then use AIC to get the Akaike information criterion value for this new model:
AIC(model.lm4)
[1] 551.3252With this value we can now see that, not only is this not a better fit than our current best model that has an AIC value of 549.2017, but this new model is a lower fit than a model that includes all of the variables, model.lm.
It should be noted that using AIC to compare models does not operate in the same way as testing a null hypothesis. Therefore, if all the models are a poor fit then you may only select the best of a bad bunch, so care must be taken when using this method.
Analysis of Variance (ANOVA)
The second topic I want to cover this time around is Analysis of Variance, or ANOVA, a family of statistical tests that are used when your dependent variable(s) are categorical (data are classed in groups such as gender) rather than continuous (measurements on a continuous scale such as height or weight) as it would be if you were using a regression analysis. There are several other types of analysis that are related to ANOVA which I will not cover at the moment, with increasingly long acronyms such as Analysis of Covariance (ANCOVA), Multivariate Analysis of Variance (MANOVA) and Multivariate Analysis of Covariance (MANCOVA).
In the case of ANOVA, let’s say you’ve collected a series of measurements across several samples, such as different taxa, and you want to know whether they differ significantly; in this case using an ANOVA would be the appropriate method. The null hypothesis (H0 ) for an ANOVA is as follows:
\[H_0 : \text{all samples are taken from populations with equal means}\]
As with all statistical tests there are a series of assumptions that the data must adhere to in order for the results of that analysis to be considered valid and accurate. For ANOVA they are as follows:
- [i] The data must be normally distributed.
- [ii] All the samples should have the same variance.
- [iii] The samples are randomly selected and random of each other.
There are two commonly used ANOVA tests, one-way and two-way ANOVA. The distinction between these is that in the one-way ANOVA there is only one independent variable, in this case the different taxa we are comparing, whereas in the two-way ANOVA there can be multiple independent variables. In this latter case you may wish to know whether there is an interaction between two variables on your dependent variable. Here I will focus solely on the one-way ANOVA. We will ask the question whether there is a significant difference in the size distributions of four taxa using the dataset called anova.txt available at:
As always, the first step is to load the file into the R environment, saving the data as the new variable anova (see the first article in Newsletter 85 if you are unsure of how to go about this):
anova <- read.table(file="anova.txt",header=TRUE)This file contains a matrix of two columns representing the size and taxon name, respectively, for 200 individual specimens.
Just a reminder: you can have R return the names of the columns of the variable anova:
names(anova)
[1] “size” “taxon”and if you want a description of the contents of each of the variables you can use:
summary(anova)This will provide the five-point summary (i.e. minimum, 1st quartile, median, 3rd quartile, maximum) plus the mean value for the size variable and the number of occurrences of each taxon name in the taxon variable; in this case you can tell that there are fifty rows for each of the four genera represented here.
size taxon
Min. :10.41 Taxon A:50
1st Qu. :20.26 Taxon B:50
Median :24.28 Taxon C:50
Mean :24.65 Taxon D:50
3rd Qu. :28.52
Max. :39.81The next step should always be to plot your data to check for any anomalies, i.e. outliers. Given that here we have a series of categories containing a continuous variable, a boxplot (or box and whisker) is the most appropriate way to display these data. Below is the code to produce the boxplot in Figure 5.2 that shows the distribution of sizes of our four taxa. It should be noted that the same result can be achieved if, rather than using the function boxplot, you use plot instead.
boxplot(anova$size ~ anova$taxon, xlab="Taxon", ylab="Length", notch=TRUE)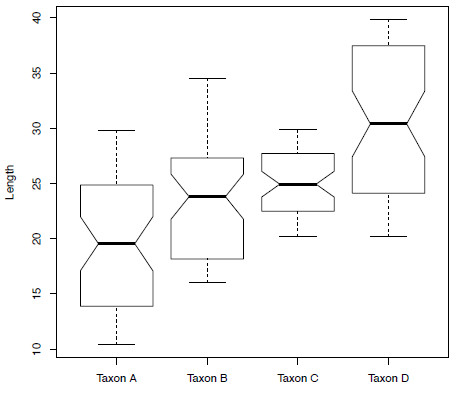
Figure 2. Boxplots showing the size distribution of the four taxa contained within the variable anova.
ANOVA, the t-test and Type I errors
Before I go through the implementation of the one-way ANOVA, I want to take a moment to explain in greater detail one aspect of the ANOVA. As I mentioned, the ANOVA test is used to see whether there are significant differences in the mean values across two or more populations. If this sounds familiar, it may be because it is the same hypothesis tested when using a t-test (see Part 1 in Newsletter 87). Therefore, performing an ANOVA on only two populations is equivalent to using a t-test on the same data. So why don’t we just use a t-test on three pairs of anova datasets, for example, (e.g. Taxon A/Taxon B, Taxon B/Taxon C, Taxon A/Taxon C) and that should provide the same result, shouldn’t it? The reason that it won’t is that, by performing separate t-tests, we risk inflating the probabilities of making a Type I error. This, in simple terms, is when you determine that the results are significant when in fact they are not. This is opposed to a Type II error, whereby a genuine effect is rejected when it shouldn’t have been.
Coming back to our three-population problem, if we use a significance (or alpha) value of 0.05 (i.e. p-values < 0.05 are considered significant), in each case the chance of not making a Type I error is 0.95. Because we have three comparisons in this case we multiply the probabilities together, i.e. 0.95*0.95*0.95, which equals 0.857. So, in order to get the probability of making a Type I error we subtract this value from 1, which gives a new alpha value of 0.143 or 14.3%. This is much higher than most scientists would require for an acceptable result. However, when using the ANOVA function in R it controls for this effect and keeps the alpha value at 0.05. It is important to say here that while you can never completely eliminate the chances of making a Type I error you can have some control over the likelihood of it occurring, therefore controlling that your results are not simply down to chance.
Back to ANOVA
Now, getting back to running our ANOVA analysis on the four taxa. The model formulae are the same as for the linear regression with the dependent variable first, in this case size, followed by the independent variables, here taxon.
aov.mod <- lm(anova$size ~ anova$taxon)You can use the function aov to the same effect:
aov.mod <- aov(anova$size ~ anova$taxon)We can also run the same model by using just the variable names, providing we tell aov the name of the dataset:
aov.mod <- lm(size ~ taxon, data=anova)The next step is to use the function anova to get the ANOVA table which produces all of the test‑statistics:
anova(aov.mod)Analysis of Variance Table Response: size Df Sum Sq Mean Sq F value Pr(>F) Taxon 3 3151.9 1050.64 37.531 < 2.2e-16 *** Residuals 196 5486.8 27.99 --- Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
The two important numbers here are the test statistic (F value) and the p-value. You can see from this result, with a p-value < 0.05, that across the anova dataset there are significant differences amongst the four taxa. Obviously this does not tell you whether all the pairs of genera are significantly different, so we can apply Tukey’s honestly significant difference (HSD) test using the function TukeyHSD:
TukeyHSD(aov(aov.mod))
Tukey multiple comparisons of means
95% family-wise confidence level
Fit: aov(formula = aov.mod)
$taxon
diff lwr upr p adj
Taxon B-Taxon A 4.350773 1.608800 7.092745 0.0003348
Taxon C-Taxon A 5.642761 2.900789 8.384733 0.0000016
Taxon D-Taxon A 11.125072 8.383100 13.867045 0.0000000
Taxon C-Taxon B 1.291988 -1.449984 4.033961 0.6143048
Taxon D-Taxon B 6.774300 4.032327 9.516272 0.0000000
Taxon D-Taxon C 5.482311 2.740339 8.224284 0.0000033This will print a list of all the different pairs of taxa along with corrected p-values (p adj) in each case. According to this result, all the different pairs of taxa are significantly different with the exception of Taxon B and Taxon C. If we look again at Figure 5.2 any lack of overlap in the notches that are placed at the median signify a significant difference. Taxon B and Taxon C show a lot of overlap in the notches whereas this is not true of all other taxon pairings.
As with the regression analysis in Part 2, Newsletter 89, we should also check that the result doesn’t violate the model assumptions (Figure 5.3). Is this the best model to use for this data?
par(mfrow=c(2,2))
plot(aov.mod)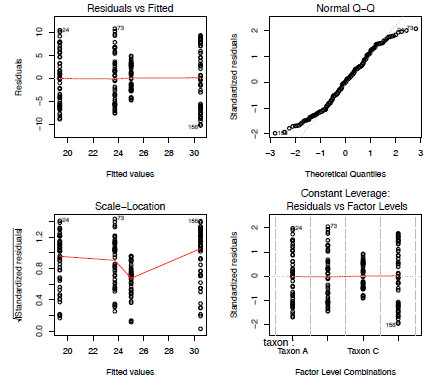
Figure 3. The four model-checking plots from the fitting of a one-way ANOVA model to the anova dataset.
Summary
By the end of this second article concerning statistical modelling I hope that you will be at home working in the R environment and be comfortable loading in your own data and conducting basic statistical analyses ranging from one- and two-sample tests to correlations and modelling. For the moment this is where I will leave these kinds of analyses; however, they will no doubt crop up again from time to time. At the very least, my primary intention so far has been to convince anyone who has been wary about learning the art of programming that it is not as complicated or as scary as you may have once thought, and that it doesn’t take a lot of work to perform the most basic of tasks.
In the next part of this series I will move into applied methods that are commonly used by palaeontologists, such as data visualization, phylogenetics and multivariate methods. Up until now I have avoided the use of the many packages that are currently available for R users, choosing to restrict my discussion to functions that are available with the basic setup of R. Starting with the next article I will begin to explore some of these packages that make more specific analyses available to us.
References
ALROY, J. 2010. Fair sampling of taxonomic richness and unbiased estimation of origination and extinction rates. In ALROY, J. and HUNT, G. (eds.) Quantitative Methods in Paleobiology. The Palaeontological Society Papers, 16, 55–80.
Further Reading
Crawley, M. J. 2005. Statistics: an introduction using R. John Wiley and Sons, New Jersey. 342 pp.
Field, A., Miles, J. and Field, Z. 2012. Discovering statistics using R. SAGE publications Ltd, New York. 992 pp.
